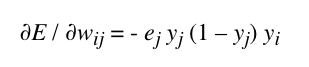11 minutes
Programmer un réseau de neurones en JavaScript
Pour bien comprendre comment fonctionnent les réseaux de neurones, nous allons en créer un from scratch en JavaScript. Je pense que c’est intéressant d’en créer un de toute pièce avant de s’attaquer à des réseaux de neurones profonds ou d’utiliser des frameworks qui masquent toute la complexité.
Introduction
Un neurone biologique est composé d’un corps cellulaire, d’un réseau de dendrites et d’un axone.
- Le corps cellulaire contient le patrimoine génétique.
- Les signaux électriques transitent par le réseau de dendrites. Ces dernières correspondent aux entrées du neurone.
- L’axone à la sortie du neurone permet de véhiculer l’influx nerveux.
Les neurones artificiels s’inspirent du comportement des neurones biologiques; c’est-à-dire de leur capacité à s’activer à partir d’un seuil.
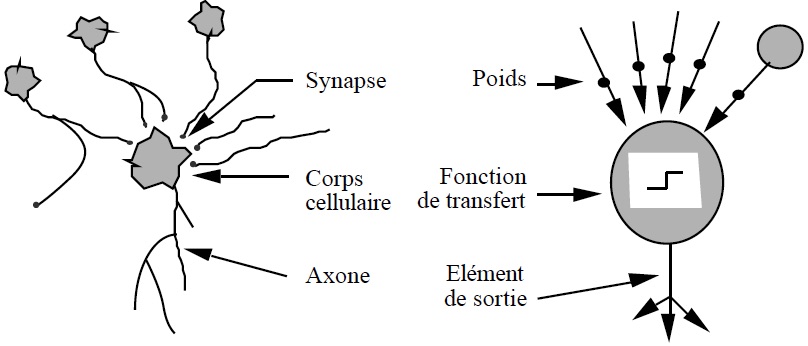
Si on entre plus dans le détail, un neurone calcule la somme pondérée de ses entrées, puis il compare le résultat à un seuil (dit seuil d’activation). Basiquement, si la somme est supérieure au seuil, alors il s’active et sort la valeur 1. Réciproquement, si la somme est inférieure au seuil, alors il ne s’active pas et sort la valeur 0.
En ce qui concerne la somme pondérée, chaque entrée valant 0 ou 1 est multipliée par un coefficient qui représente son poids (on parle de poids synaptique). A noter, que si un signal d’entrée est à 1, alors la valeur ce ce signal prend tout simplement la valeur du coefficient. De même, si le signal d’entrée est à 0, alors sa valeur reste à 0.
Un neurone fonctionne ainsi: il faut additionner toutes les valeurs obtenues par les sommes pondérées en entrée et comparer le résultat à la valeur d’un seuil.
Précision sur les seuils d’activation
Nous venons de voir dans le paragraphe précédent que la sortie d’un neurone nous donnait 1 ou 0 en fonction du seuil d’activation. C’est tout à fait vrai lorsqu’on utilise une fonction à seuil binaire. Mais en pratique on utilise d’autres fonctions d’activation nous donnant des valeurs numériques comprises entre 0 et 1. La plus répandue est la “fonction sigmoïde” (aussi appelée “fonction logistique” ou “courbe en S”).
Avec cette fonction, le passage de 0 à 1 est plus progressif comme on peut le voir sur la courbe suivante:
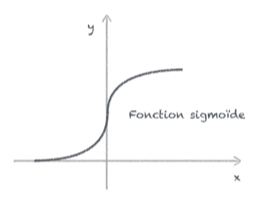
L’équation de la fonction sigmoïde est la suivante:
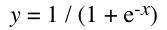
Initialisation de notre réseau de neurones
Nous allons créer un réseau simple permettant de résoudre un problème simple. Nous allons classifier en 4 catégories des images noir et blanc réduites à seulement 4 pixels. C’est un exemple pédagagique bien sûr.
Pendant la phase d’apprentissage, nous allons présenter au réseau les images que l’on souhaite reconnaître. Puis pendant la phase de reconnaissance, on présente des images aléatoires afin de vérifier si le réseau a bien appris.
Voici les images dont on va se servir pour entraîner notre réseau.

Pour se simplifier la vie, nous allons représenter ces images sous forme de tableau.
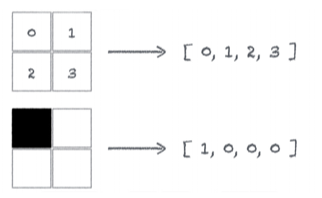
Nous allons les représenter les 4 catégories d’images via un tableau à 2 valeurs.
- [0, 0] pour les images n’ayant aucun ou tous les pixels noirs
- [0, 1] pour les images comprenant 1 pixel noir
- [1, 0] pour les images comprenant 2 pixels noirs
- [1, 1] pour les images comprenant 3 pixels noirs
Nous allons construire un réseau comprenant 3 couches:
- La première couche (couche d’entrée) contient 4 neurones en entrée pour les 4 pixels de l’image.
- La deuxième couche est une couche cachée. Elle permet de faire la liaison entre la couche d’entrée et la couche de sortie.
- La 3ème couche (couche de sortie) contient 2 neurones pour les 2 valeurs représentant notre catégorie.
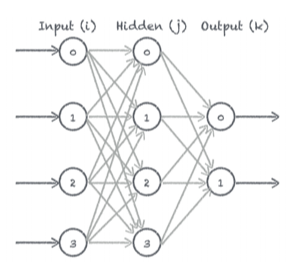
Pour construire un réseau de neurones avec une structure simple comme celle-ci, il suffit d’assembler les neurones les uns derrières les autres. On connecte les sorties des uns aux entrées des autres. Entre chaque couche, nous relions les sorties des neurones de la couche précédente à tous les neurones de la couche suivante. Dans notre exemple simple, on appelle ce genre de réseau un réseau totalement connecté.
En JavaScript, on initialise les couches du réseau via des tableaux:
let input = [];
let hidden = [];
let output = [];
En plus de ces tableaux, il nous en faut 2 autres pour stocker les valeurs des poids synaptiques associés aux connexions entre la 1ère et 2ème couches et la 2ème et 3ème couches:
let Wh = [];
let Wo = [];
On va créer un dernier tableau pour notre input:
// Tableau représentant notre image en input
let inputData = [0, 1, 0, 1]
On crée une fonction d’initialisation des différents tableaux.
const reset = () => {
input = [0, 0, 0, 0];
hidden = [0, 0, 0, 0];
output = [0, 0];
// 0.5 a été choisi totalement arbitrairement
// En pratique, on aurait pu générer des valeurs aléatoires distribuées uniformément sur l'intervalle [-1; 1] et dont la moyenne aurait été nulle.
Wh = [[0.5, 0.5, 0.5, 0.5],
[0.5, 0.5, 0.5, 0.5],
[0.5, 0.5, 0.5, 0.5]
[0.5, 0.5, 0.5, 0.5]];
Wo = [[0.5, 0.5, 0.5, 0.5],
[0.5, 0.5, 0.5, 0.5]];
}
Chaque neurone de la couche d’entrée est connecté à tous les neurones de la couche cachée. Par conséquent, il y aura 4 poids synaptiques à prendre en compte dans le calcul de la moyenne pondérée pour chaque neurone de la couche cachée. Wh contient donc 4 tableaux de 4 poids.
Pour Wo, on a 2 neurones dans la couche de sortie. Donc on a 2 tableaux. Ces 2 tableaux contiennent les 4 poids de la couche cachée.
Propagation des données
Les données d’input sont propagées dans le réseau de neurones. Pour propager les données de la couche d’entrée vers la couche de sortie, il faut réaliser une succession de calculs de couche en couche et de neurone en neurone. Ces calculs sont simples car ce ne sont que des multiplications et des additions. Par contre, il faut en faire beaucoup. Nous n’allons pas détailler les calculs car cela n’a pas d’intérêt et c’est fastidieux. On va plutôt utiliser des matrices et faire des produits matriciels…
Nous allons commencer par créer notre fonction sigmoïde qui permettra de calculer la valeur de sortie des neurones.
const sigmoid = (x) => {
return 1 / (1 + Math.pow(Math.E, (-1 * x)));
}
En programmation, si on veut connecter deux couches de neurones (par exemple connecter la couche A avec la couche B), voici le pseudo-code:
Pour chaque neurone de la couche B:
Pour chaque neurone de la couche A:
Calcul sur le lien Wba;
Fin pour;
Fin pour;
En JavaScript, cela donne:
for (let j = 0; j < B.length; j++) {
for (let i = 0; j < A.length; i++) {
// Calcul sur le lien w[j][i]
}
}
Après ces quelques explications, nous allons créer une fonction de propagation des données de la couche d’entrée vers la couche de sortie. Cette fonction va appliquer la fonction d’activation sur les sommes pondérées calculées entre les neurones des différentes couches. On va créer une fonction appelée propagate().
const propagate = (d) => {
// On copie les données dans la couche d'entrée
for (let i = 0; i < input.length; i++) {
input[i] = d[i];
}
// On propage dans la couche cachée
// Xh contient les sommes cumulées pour la couche cachée
Xh = [0, 0, 0, 0];
for (let j = 0; j < hidden.length; j++) {
for (let i = 0; i < input.length; i++) {
Xh[j] += Wh[j][i] * input[i];
}
}
// On applique la fonction d'activation
for (let j = 0; j < hidden.length; j++) {
hidden[j] = sigmoid(Xh[j]);
}
// On propage dans la couche de sortie
// Xo contient les sommes pondérées de chaque neurone de sortie
Xo = [0, 0];
for (let k = 0; k < output.length; k++) {
for (let j = 0; j < hidden.length; j++) {
Xo[k] += Wo[k][j] * hidden[j];
}
}
// On applique la fonction d'activation
for (let k = 0; k < output.length; k++) {
output[k] = sigmoid(Xo[k]);
}
}
Test de la propagation
On va créer une petite interface en HTML permettant de visualiser la propagation. Si la valeur des 2 neurones de la dernière couche ont une valeur différente de [0, 0] (valeur d’initialisation), c’est que la propagation des données s’est bien produite.
Apprentissage
Nous allons passer à la phase la plus importante qui est l’apprentissage. Cette phase est indispensable pour que notre réseau puisse apprendre à reconnaître nos images. Nous allons créer une fonction learn() qui implémente l’algorithme de rétropropagation du gradient de l’erreur.
On va commencer par créer 2 nouvelles variables qui vont nous servir à définir le taux d’apprentissage et à définir la cible que l’on souhaite obtenir en sortie du réseau de neurones.
- Le taux d’apprentissage va être initialisé à 0.5 et sera représenté par la variable alpha.
- La cible est un tableau de 2 valeurs. Il va être initialisé à [0, 0] et s’appelera target. Il s’agit de la cible à atteindre pour nos neurones de sortie.
let alpha = 0.5;
let target = [0, 0];
Nous allons passer à l’implémentation de l’algorithme de rétropropagation du gradient de l’erreur. Pour notre exemple, cet algorithme comporte 4 étapes qui sont exécutées les unes à la suite des autres de manière cyclique. La boucle s’arrête lorsqu’un critère d’arrêt est atteint. On considère donc que l’apprentissage est terminé. Le critère d’arrêt peut être soit un seuil d’erreur atteint ou soit un nombre d’itérations maximum atteint.
Les 4 étapes de l’algorithme sont les suivantes:
- Calcul de l’erreur en sortie de la propagation des données.
- Calcul des gradients d’erreurs pour corriger les poids synaptiques des neurones de la couche de sortie.
Voici la formule que nous coderons qui permet de calculer l’erreur propagée:
- Calcul des gradients d’erreurs pour corriger les poids synaptiques des neurones de la couche cachée.
- Mise à jour des poids synaptiques de la couche de sortie et de la couche cachée
Ci dessous, le code JavaScript qui implémente cet algorithme:
const learn = () => {
// 1ère étage:
// On calcule l'erreur sur les neurones de sortie
let error = [];
for (let k = 0; k < output.length; k++) {
error[k] = target[k] - output[k]
}
// 2ème étage:
// Calcul des gradients d'erreurs de la couche de sortie
let gradErrOutput = [[0, 0, 0, 0], [0, 0, 0, 0]];
for (let k = 0; k < output.length; k++) {
for (let j = 0; j < hidden.length; j++) {
gradErrOutput[k][j] = -error[k] * output[k] * ( 1 - output[k]) * hidden[j];
}
}
// 3ème étage:
// a.
// On retropropage l'erreur de sortie vers les neurones de la couche cachée proportionnellement à leurs poids synaptiques
// b.
// Ensuite on calcule les gradients d'erreurs dans la couche cachée
let gradErrHidden = [[0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0], [0, 0, 0, 0]];
for (let j = 0; j < hidden.length; j++) {
for (let i = 0; i < input.length; i++) {
// Variable locale permettant de cumuler l'erreur proportionnellement aux poids synaptiques
let e = 0;
for (k = 0; k < output.length; k++) {
// Rappel:
// Wo contient les poids synaptiques associés aux connexions entre la 2ème et 3ème couches
e += Wo[k][j] * error[k];
gradErrHidden[j][i] = -e * hidden[j] * (1 - hidden[j]) * input[i];
}
}
}
// 4ème étape:
// Mise à jour de l'ensemble des poids synaptiques. Pour chaque poids, on soustrait une portion du gradient d'erreur par application du taux d'apprentissage alpha.
for (let k = 0; k < output.length; k++) {
for (let j = 0; j < hidden.length; j++) {
Wo[k][j] -= alpha * gradErrOutput[k][j];
}
}
for (let j = 0; j < hidden.length; j++) {
for (let i = 0; i < input.length; i++) {
Wh[j][i] -= alpha * gradErrHidden[j][i];
}
}
}
Test de la rétropropagation
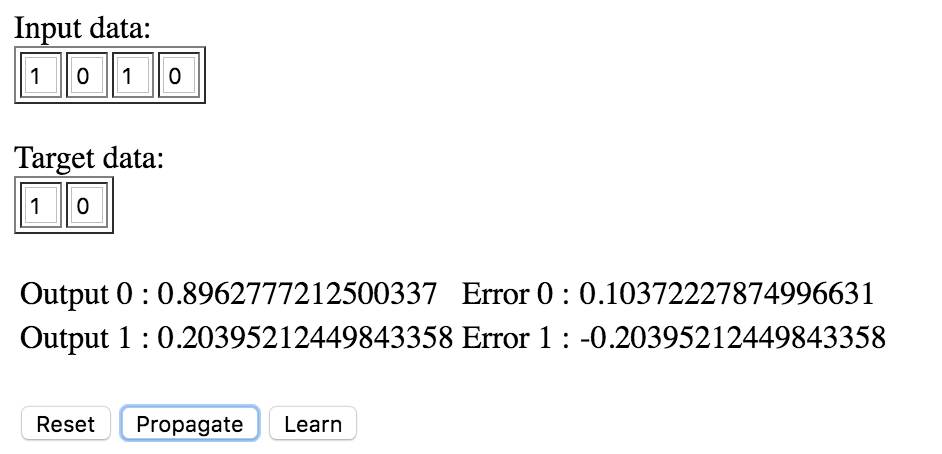
Nous allons modifier l’interface que nous avons précédemment codée afin de tester le bon fonctionnement de notre algorithme.
Tout le code est accessible ci-dessous:
Si vous appuyez une dizaine de fois sur les boutons Propagate et Learn alternativement, vous verrez que le réseau de neurones fonctionne bien. Les erreurs diminuent et les valeurs en output convergent bien vers [1, 0].
Conclusion
Si vous prenez le temps de bien lire cet article et de recoder l’ensemble du réseau de neurones, vous comprendrez comment ils fonctionnent. Bien comprendre ces réseaux simples est indispensable pour aller plus loin et faire du Deep Learning. L’implémentation de notre réseau pour notre exemple simple était trivial. Par contre, en pratique, les use cases sont beaucoup plus complexes et donc cela se corse rapidement car l’algorithme de rétropropagation du gradient de l’erreur est sensible aux conditions de son exécution. Il faudra faire attention au surapprentissage (overfitting) et à la disparition du gradient (vanishing gradient) en jouant sur les fonctions d’activation, le taux d’apprentissage, pré-traiter les données d’entrée en les normalisant par exemple…