Evaluer ses modèles de classification

Introduction

Voici les métriques à analyser pour évaluer la performance de son modèle.

Classification

Justesse / Accuracy

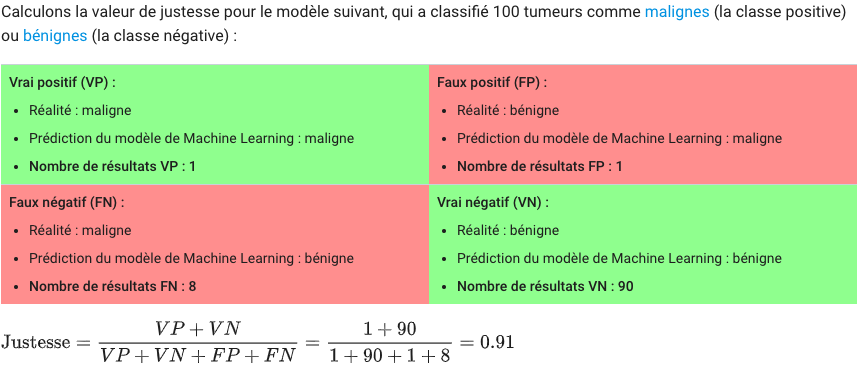
• Justesse, (ou Taux de réussite ou encore taux de prédiction; accuracy en anglais). Mais attention, il ne faut pas se fier qu’à cette seule métrique.

  Pour la calculer, c’est simple: accuracy = justesse (%) = nombre de prédictions correctes / (nombre total de prédictions données * 100)

  ou accuracy = justesse = VP + VN / ( VP + VN + FP + FN )

Exemple (source developer.google.com):

• CART (Classification And Regression Tree) Voir wikipédia: http://en.wikipedia.org/wiki/Predictive_analytics#Classification_and_regression_trees

Matrice de confusion

• La Matrice de confusion (tableau de contingence; contingency table en anglais) est une manière simple et non ambigue de présenter les résultats d’un classifier. (Voici un exemple sur ce notebook: https://leandeep.com/datalab-own/analyse-donnees-dataset-desequilibre.htm)

  Pour un sujet de classification binaire et non multi-classes (comme l’example plus haut), la matrice de confusion ressemble à ceci:

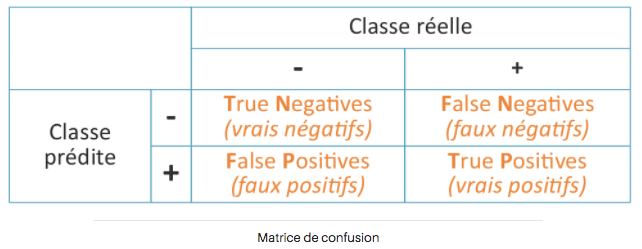
En haut, on a ce qui est observé et sur le côté ce qui est prédit.

Parfois et par exemple pour des sujets où les classes sont déséquilibrées il vaut mieux ne pas se fier au taux de précision (accuracy) et plus utiliser une matrice de confusion.

En effet, utiliser le nombre de faux positifs ou faux négatifs pour les sujets liés à la santé par exemple a plus de sens que le taux de précision du modèle. Un modèle qui prédit si oui ou non on a le cancer ne doit pas avoir de faux négatif. Le taux de précision a donc moins d’importance dans ce cas. Au contraire, un modèle qui prédit qu’un patient est en bonne santé alors qu’il a un cancer c’est grave car le patient peut en mourir puisqu’il ne sera pas soigné !)

Precision

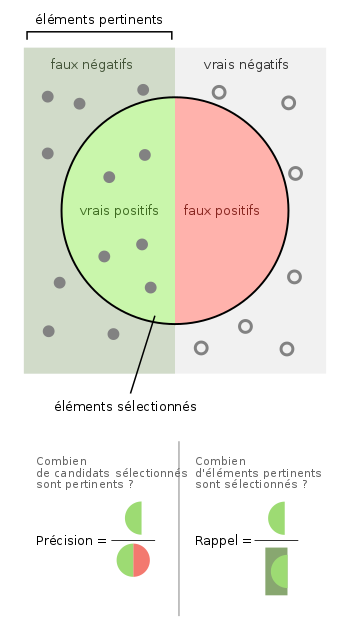
La précision permet de répondre à la question: “Quelle proportion d’identifications positives était effectivement correcte ?”

La précision se calcule comme ceci:

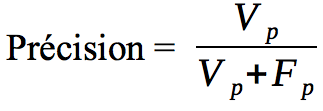
Example (source developer.google.com):

**Rappel **

Le rappel (recall en anglais ou aussi sensibilité ou encore taux de vrais positifs (TVP)) permet de répondre à la question suivante: “Quelle proportion de résultats positifs réels a été identifiée correctement ?”

Le rappel se calcule comme ceci:

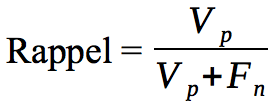
Example (source developer.google.com):

Pour évaluer les performances d’un modèle de façon complète, vous devez analyser à la fois la précision et le rappel. Malheureusement, précision et rappel sont fréquemment en tension. Ceci est dû au fait que l’amélioration de la précision se fait généralement au détriment du rappel et réciproquement.

Dans l’exemple du dépistage de cancer c’est la proportion de vrais positifs parmi les personnes à dépister.

**Spécificité **

La spécificité se calcule comme ceci:

Dans l’exemple du dépistage du cancer c’est proportion de vrais négatifs chez les non-malades.

Différence avec la sensibilité:

La sensibilité est l’indice qui évalue la capacité d’une mesure à bien classer les malades (ou les exposés), et la spécificité celui qui évalue la capacité à bien classer les non-malades (ou les non-exposés).

**Score F1 **

Aussi appelé F Score ou F Measure, le score F1 permet de traduire l’équilibre entre la précision et le rappel. Attention, le problème de cette métrique est qu’elle ne tient pas compte de l’éventuel déséquilibre entre les classes.

Il se calcule comme ceci:

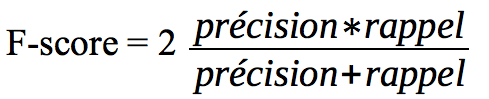
Courbe ROC

La courbe ROC (Receiver Operating Characteristic) trace le taux de vrais positifs en fonction du taux de faux positifs.

Le taux de vrais positifs (TVP) est l’équivalent du rappel.

Le taux de faux positifs (TFP) se calcule comme ceci:

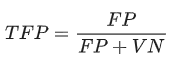
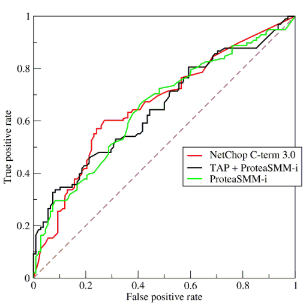
Elle résume le trade-off entre le taux de vrais positifs et le taux de faux négatifs pour un modèle prédictif en utilisant différent seuils de probabilité.

Cette courbe sert également à comparer différents classifieurs. Plus une courbe a des valeurs élevées, plus l’aire sous la courbe est grande, moins le classifieur fait d’erreur.

Il existe aussi la Precision-Recall curves. The latter summarizes the trade-off between the true positive rate and the positive predictive value for a predictive model using different probability thresholds.

ROC curves are appropriate when the observations are balanced between each class, whereas precision-recall curves are appropriate for imbalanced datasets. En savoir plus sur cet article: https://machinelearningmastery.com/roc-curves-and-precision-recall-curves-for-classification-in-python/

AUC

En savoir plus sur l’aire sous la courbe ROC (AUC pour Area Under the Curve ROC) sur le même site qu’au dessus: https://machinelearningmastery.com/roc-curves-and-precision-recall-curves-for-classification-in-python/

“An excellent model has AUC near to the 1 which means it has good measure of separability. A poor model has AUC near to the 0 which means it has worst measure of separability. And when AUC is 0.5, it means model has no class separation capacity whatsoever. It would be a naive model.”

En gros l’AUC correspond à l’intégrale de la fonction ROC.

Voici une vidéo explicative: https://www.dataschool.io/roc-curves-and-auc-explained/

Conclusion

Un “bon” classifieur doit présenter d’une part un rappel élevé et, d’autre part, une précision et une spécificité élevée (et un taux de faux positifs faible).

Scikit Learn fournit un tas de métriques par défaut: https://scikit-learn.org/stable/modules/model_evaluation.html

Voici enfin un article intéressant sur les métriques en général pour des sujets de classification, de recommandation et de régression. https://www.oreilly.com/ideas/evaluating-machine-learning-models/page/3/evaluation-metrics