Introduction

Miser sur la corrélation entre différents assets pour faire du pair trading est une mauvaise idée. Il vaut mieux miser sur la cointégration.

Corrélation vs Cointégration

La cointégration est une relation statistique entre deux variables qui évoluent de manière similaire à long terme. Cela signifie que si l’une des variables change, l’autre suivra également cette tendance sur une période de temps prolongée.

La corrélation, en revanche, mesure simplement la relation entre deux variables à un moment donné. Si deux variables sont corrélées, cela signifie qu’elles varient de manière similaire, mais cela ne garantit pas qu’elles continueront de le faire à long terme.

En résumé, la cointégration implique une relation à long terme entre deux variables, tandis que la corrélation ne mesure que la relation à un moment donné. Dans cet article, nous allons donc approfondir le concept de cointégration.

Cointégration

Cointégration

La cointégration est donc une relation à long terme entre deux séries de données qui évoluent de manière similaire sur une période de temps prolongée.

Spread

Pour rappel, un spread est la différence entre les valeurs de deux séries de données. On va donc rechercher un spread qui franchit zéro pour acheter ou vendre des pairs; pour trader.

Z-score

Le z-score est une mesure statistique qui indique si une valeur est éloignée ou proche de la moyenne des valeurs d’une série de données.

En d’autres termes, le z-score est une mesure de l’écart entre une valeur et la moyenne (ou espérance) d’une distribution de données. Plus précisément, si X est une variable aléatoire suivant une distribution normale de moyenne μ et de déviation standard σ, le z-score de X est donné par la formule suivante :

z = (X - μ) / σ

Par exemple, si la moyenne des notes d’un examen est de 70 et que la déviation standard est de 5, et si vous obtenez une note de 80, votre z-score sera de (80 - 70) / 5 = 2.

Le z-score peut être utilisé pour évaluer si une valeur est “normale” ou “anormale” par rapport à la distribution des données.

Par exemple, si la moyenne des tailles d’une population est de 1,75 m et que la déviation standard est de 0,1 m, on peut dire qu’une personne mesurant 1,90 m a un z-score de (1,90 - 1,75) / 0,1 = 2, ce qui signifie qu’elle est 2 écarts-types au-dessus de la moyenne.

On peut également utiliser les z-scores pour faire des prévisions sur les valeurs futurs, en utilisant la loi normale.

Vulgairement, le Z-Score nous indique à quelle distance se situe un point de la moyenne.

En utilisant ces trois termes ensemble, nous pouvons comprendre comment la cointégration peut être utilisée pour mesurer l’écart entre deux séries de données et déterminer si cet écart est statistiquement significatif.

Par exemple, si nous avons deux séries de données qui sont cointégrées, nous pouvons utiliser le spread pour mesurer l’écart entre elles et le z-score pour savoir si cet écart est significatif.

Si le z-score est élevé, cela signifie que l’écart entre les deux séries de données est important et pourrait être utilisé pour ouvrir une position.

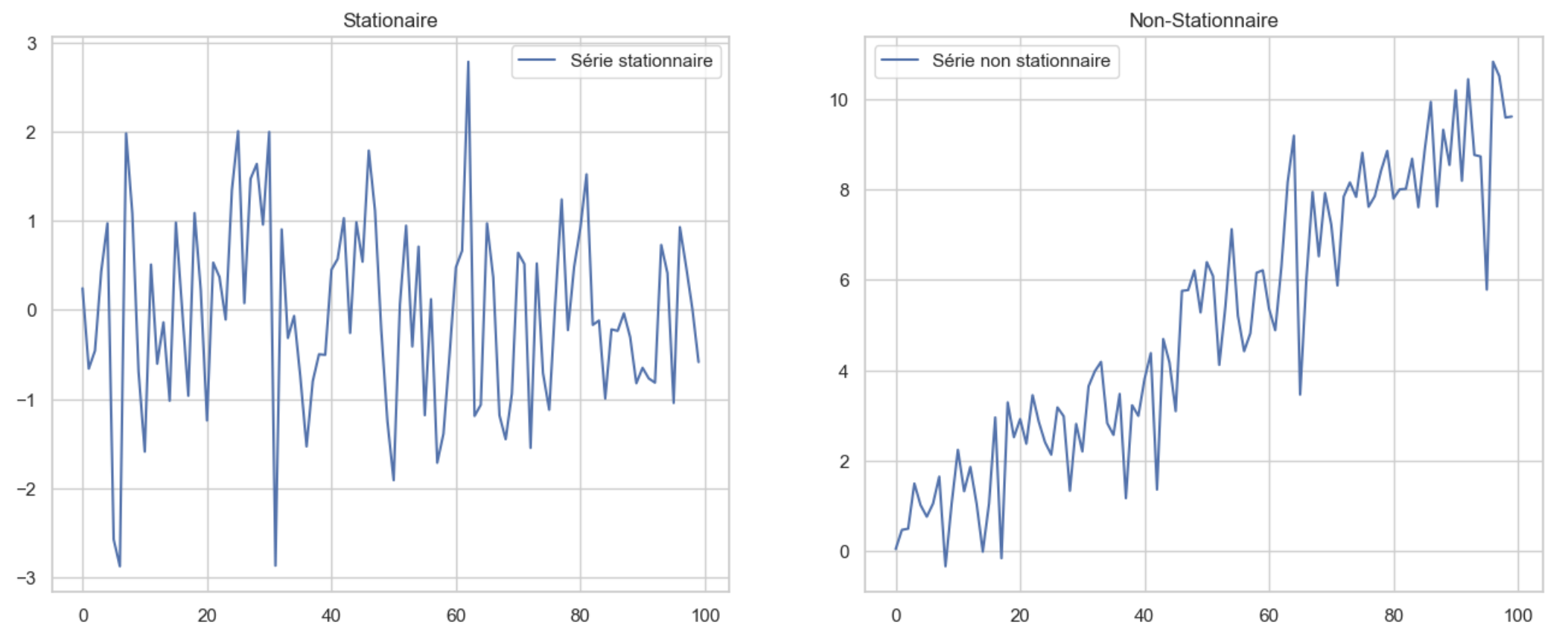
Importance de la stationnarité

Une courbe stationnaire en trading est une courbe qui ne montre pas de tendance claire ni de variation significative de prix sur une période de temps donnée. Elle est souvent utilisée pour déterminer si un actif est en surachat ou en survente et peut aider les traders à prendre des décisions sur le moment opportun pour acheter ou vendre.

Une courbe stationnaire peut être le résultat d’une période de consolidation du marché, où les investisseurs hésitent à prendre des positions et où le prix reste stable.

La stationnarité est importante en trading car elle permet de prévoir de manière plus précise les mouvements futurs des prix. En effet, lorsque les données sont stationnaires, cela signifie qu’elles ont une moyenne et une variance constante au fil du temps et ne sont pas influencées par des événements externes. Cela permet de mettre en place des modèles de prévision fiables et de prendre des décisions de trading en toute confiance.

De plus, la stationnarité est importante pour éviter les erreurs de modélisation qui peuvent entraîner des pertes financières importantes. Si les données ne sont pas stationnaires, il est possible que les modèles de prévision utilisés ne soient pas adaptés et ne reflètent pas correctement les mouvements futurs des prix.

Enfin, la stationnarité est également importante car elle permet de comparer les performances des différentes stratégies de trading et de choisir celle qui est la plus adaptée. Si les données ne sont pas stationnaires, il est difficile de déterminer si une stratégie est performante ou non, car elle peut être influencée par des facteurs externes qui ne sont pas pris en compte dans les modèles de prévision.

Faire des statistiques sur des données non stationnaires peut amener à des résultats inutiles.

Déterminer si une série est stationnaire

Pour déterminer si une série temporelle est stationnaire ou non, on peut utiliser l’Augmented Dickey Fuller (ADF). La stationnarité signifie que les caractéristiques de la série temporelle, telles que la moyenne et la variance, ne varient pas au fil du temps.

Pour utiliser l’ADF, nous devons d’abord supposer qu’une série temporelle est non stationnaire et que sa moyenne et sa variance augmentent au fil du temps. Nous testons alors cette hypothèse en utilisant l’ADF et en comparant les résultats à une valeur seuil connue. Si les résultats de l’ADF sont inférieurs à la valeur seuil, cela signifie que l’hypothèse de non-stationnarité est rejetée et que la série temporelle est considérée comme stationnaire. Si les résultats de l’ADF sont supérieurs à la valeur seuil, cela signifie que l’hypothèse de non-stationnarité est acceptée et que la série temporelle est considérée comme non stationnaire.

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from statsmodels.tsa.stattools import adfuller


def generate_data(params):
    mu = params[0]
    sigma = params[1]
    return np.random.normal(mu, sigma)

def generate_series():
    params = (0, 1)
    T = 100

    Serie_stationnaire = pd.Series(index=range(T))
    Serie_stationnaire.name = 'Série stationnaire'

    for t in range(T):
        Serie_stationnaire[t] = generate_data(params)

    T = 100

    Serie_non_stationnaire = pd.Series(index=range(T))
    Serie_non_stationnaire.name = 'Série non stationnaire'

    for t in range(T):
        params = (t * 0.1, 1)
        Serie_non_stationnaire[t] = generate_data(params)
        
    fig, (ax1, ax2) = plt.subplots(nrows =1, ncols =2, figsize=(16,6))

    ax1.plot(A)
    ax2.plot(Serie_non_stationnaire)
    ax1.legend(['Série stationnaire'])
    ax2.legend(['Série non stationnaire'])
    ax1.set_title('Stationaire')
    ax2.set_title('Non-Stationnaire')
    return (Serie_stationnaire, Serie_non_stationnaire)

def stationarity_test(X, cutoff=0.01):
    pvalue = adfuller(X)[1]
    if pvalue < cutoff:
        print(f"p-value = {pvalue} La série '{X.name}' est stationnaire")
    else:
        print('p-value = {pvalue} La série '{X.name}' est non-stationnaire')

if __name__ == "__main__":
    Serie_stationnaire, Serie_non_stationnaire = generate_series()
    stationarity_test(Serie_stationnaire)
    stationarity_test(Serie_non_stationnaire)

p-value = 7.792133892275302e-08 La série 'Série stationnaire' est stationnaire p-value = 0.9499837920490491 La série 'Série non stationnaire' est non-stationnaire

Calcul cointégration

def generate_two_series_corrolated_but_not_cointegrated()
    X_returns = np.random.normal(1, 1, 100)
    Y_returns = np.random.normal(2, 1, 100)

    X_diverging = pd.Series(np.cumsum(X_returns), name='X')
    Y_diverging = pd.Series(np.cumsum(Y_returns), name='Y')


    pd.concat([X_diverging, Y_diverging], axis=1).plot(figsize=(12,6));
    plt.xlim(0, 99)


if __name__ == "__main__":
    X,Y = generate_two_series_corrolated_but_not_cointegrated()
    print('Corrélation: ' + str(X_diverging.corr(Y_diverging)))
    score, pvalue, _ = coint(X_diverging,Y_diverging)
    print('Cointégration test p-value: ' + str(pvalue))

Corrélation: 0.9984106502979461

Cointegration test p-value: 0.17832558792675923

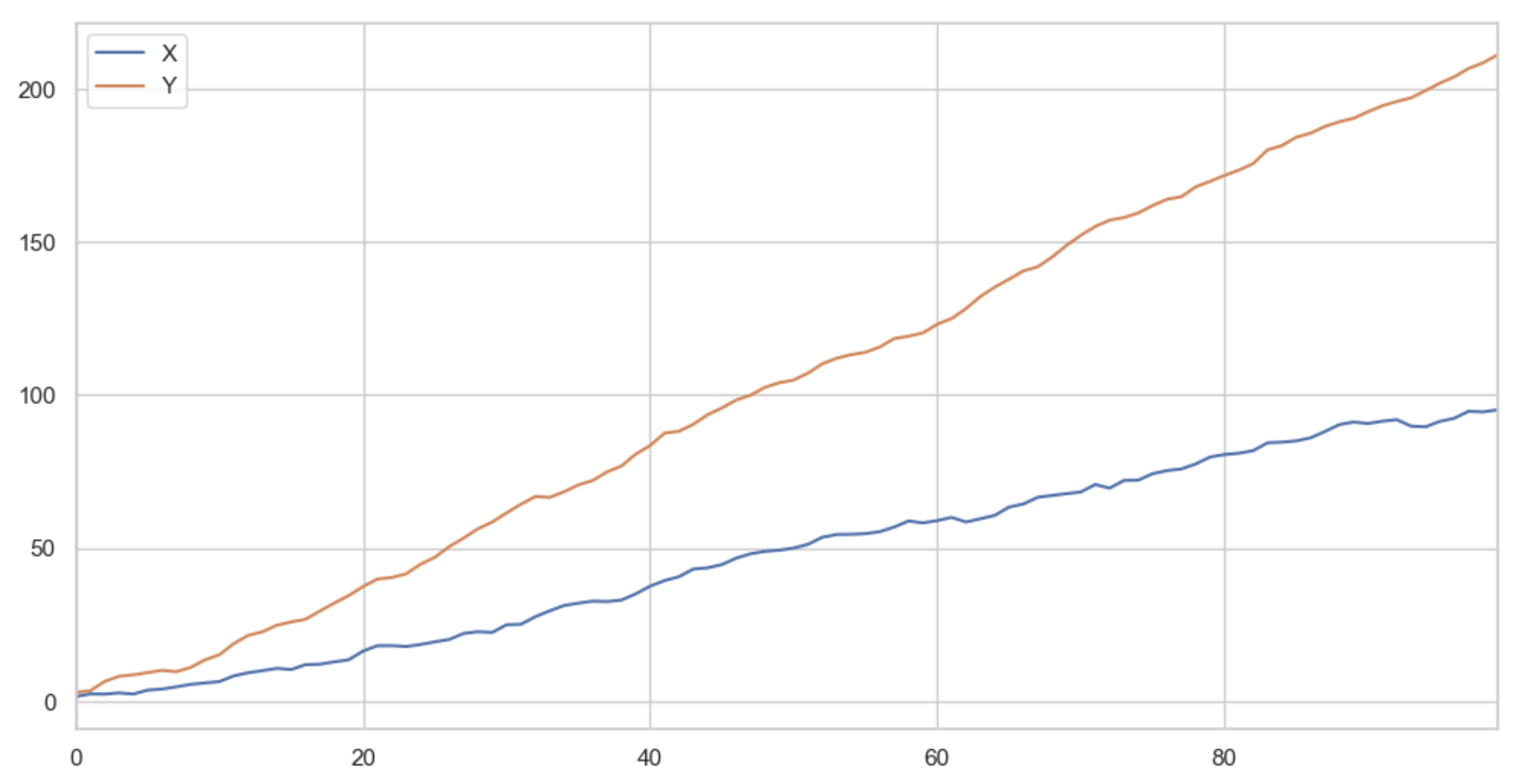
La valeur p-value nécessaire pour considérer que deux séries sont cointégrées dépend de l’hypothèse de base de l’analyse et de l’importance de la précision de l’analyse. En général, une valeur p-value inférieure à 0,05 (c’est-à-dire une probabilité inférieure à 5%) est souvent considérée comme indiquant une cointégration significative entre les deux séries. Cependant, cette valeur peut être ajustée en fonction des exigences de précision de l’analyse et de l’hypothèse de base.

Bot/Screener intéressant à créer

Voici une petite stratégie que l’on peut appeler Opportunité Z-score et que je laisse publique vous permettant de trouver des opportunités de trading.

Vous pouvez construire un screener qui analyse le Z-index sur toutes les pairs de cryptos cointégrées et qui se met à jour toutes les heures. Pour chaque pair, il suffit de prendre une timeframe de 2 semaines et un période d'1h et regarder si le z-score a bougé fortement.

Calcul du z-score

def zscore(series):
    return (series - series.mean()) / np.std(series)

Autres indicateurs

• t-value (test-value = test de valeur): Le test de valeur est utilisé pour déterminer si les deux séries peuvent être utilisées pour construire un modèle de prévision à long terme. Pour réaliser le test de valeur, on calcule d’abord une régression linéaire entre les deux séries. On peut alors utiliser un test statistique, comme le test de Durbin-Watson ou le test de Breusch-Godfrey, pour vérifier si le coefficient de la régression est significativement différent de zéro. Si le coefficient est significativement différent de zéro, cela signifie que les deux séries sont cointégrées et qu’un modèle de prévision à long terme peut être construit. Si le coefficient n’est pas significativement différent de zéro, cela signifie que les deux séries ne sont pas cointégrées et qu’un modèle de prévision à long terme ne peut pas être construit.

• c-value (critical value): C-value est une mesure de la force de la cointégration entre deux variables. Cela mesure à quel point les deux variables sont liées et dépendent l’une de l’autre à long terme. Plus le C-value est élevé, plus la cointégration est forte. Cela peut être utilisé pour évaluer la qualité de la relation entre les deux variables et pour déterminer si elles peuvent être utilisées comme base d’un modèle de cointégration.

t-value doit être inférieur à c-value.

• Hedge ratio: Le ratio de couverture est un concept utilisé pour décrire la proportion de la position d’un actif qui est couverte par une autre position dans un actif de couverture. Le ratio de couverture est généralement utilisé pour minimiser le risque d’une position en diversifiant la portefeuille. Le ratio de couverture ne garantit pas la neutralisation complète du risque, mais il peut être utilisé pour atténuer les fluctuations de la valeur de la position.