6 minutes
Tradeoff biais variance
Introduction
Le biais conduit à du sous-apprentissage (underfitting) et la variance amène du sur-apprentissage (overfitting) et donc à de hautes erreurs de tests.
Example pour un jeu de données composé de 8 points:
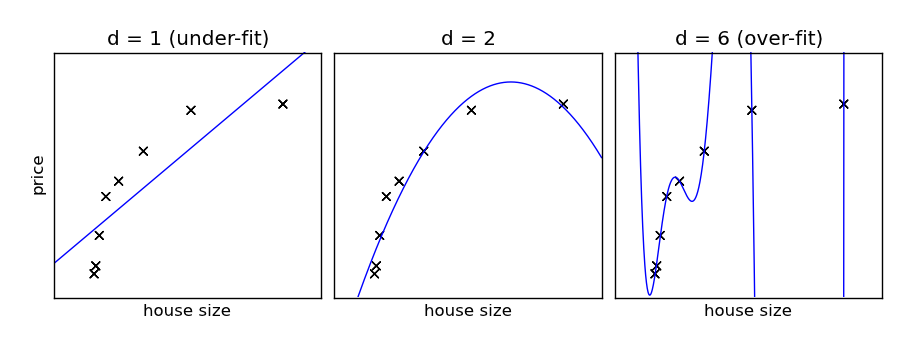
Polynomials of various degrees. d = 1 under-fits the data, while d = 6 over-fits the data.
On peut éviter cela en:
- ajoutant de la régularisation à notre modèle; ce qui va réduire la capacité de notre modèle
- Si la data est under-fit le modèle est trop simple. On dit qu’il souffre de High-bias. Le modèle est biaisé et cela se traduit par le fait que les data sont poorly fit. On pourrait trouver un autre modèle plus complexe.
- Attention au contraire à ne pas avoir un modèle trop complexe qui ferait que les données “over-fitterait” car il pourrait s’ajuster parfaitement aux données d’entrainement grâce à tous ses degrés de liberté.
- Si le modèle over-fit on peut aussi ajouter des données au dataset…
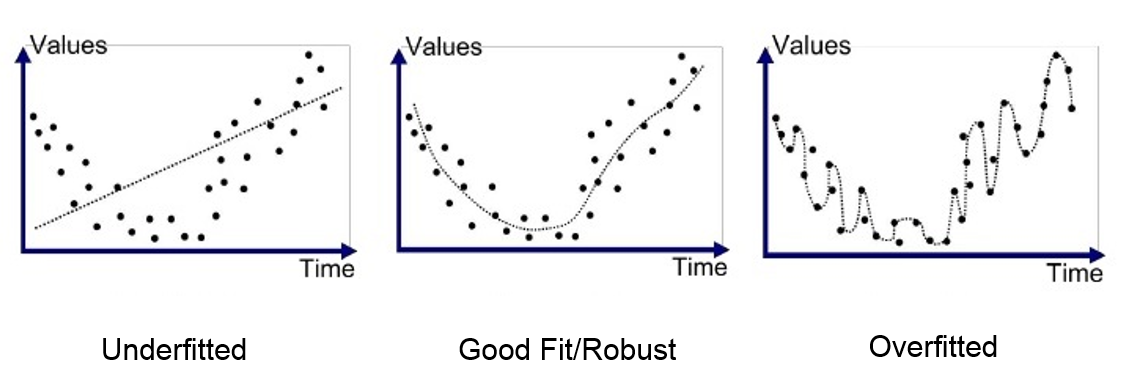
Pour déterminer le bon algorithme à utiliser par rapport à notre jeu de données, il faut pouvoir identifier quantitativement le bias et la variance pour pouvoir optimiser les metaparamètres.
C’est faisable grâce au process de cross-validation.
Détecter l’overfitting grâce à la cross-validation
Pour quantifier les effets du biais et de la variance et construire le meilleur estimateur possible, on va découper notre dataset en 3 parties:
- training set (60% du dataset)
- cross-validation set (20%)
- test set (20%)
L’idée générale est la suivante:
- Les paramètres du modèles (dans notre cas, les coefficients du polynôme) sont appris en utilisant le training set.
- L’erreur est évaluée sur le cross-validation set et les meta-paramètres (dans notre cas les degrés du polynôme) sont ajustés pour que l’erreur de cross-validation soit minimisée.
- Finalement les labels sont prédits pour le test set. Ces labels sont utilisés pour évaluer la performance de l’algorithme à labeliser des nouvelles données.
Pourquoi a-t-on besoin à la fois d’un cross-validation set et d’un test set ?
Certains data scientists utilisent les mêmes set de données pour le cross-validation set et le test set. Ce n’est pas la meilleure approche car les meta-paramètres peuvent “over-fittés” le cross-validation set tout comme les paramètres peuvent “over-fittés” le training set.
L’erreur de cross-validation de notre classifieur polynomial peut être visualisée en affichant l’erreur comme une fonction du polynôme de degré d. (Ici exemple avec 100 points)
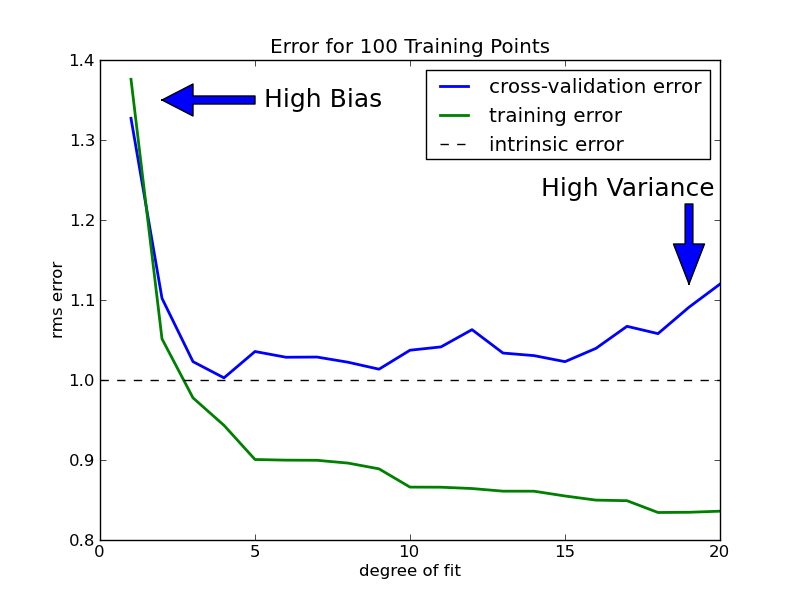
De manière générale, plus on a données d’entraînement et plus on peut utiliser un modèle complexe.
The learning curve…
La courbe d’apprentissage
La courbe d’apprentissage est l’affichage des erreurs de training et de cross-validation en fonction du nombre de training points.
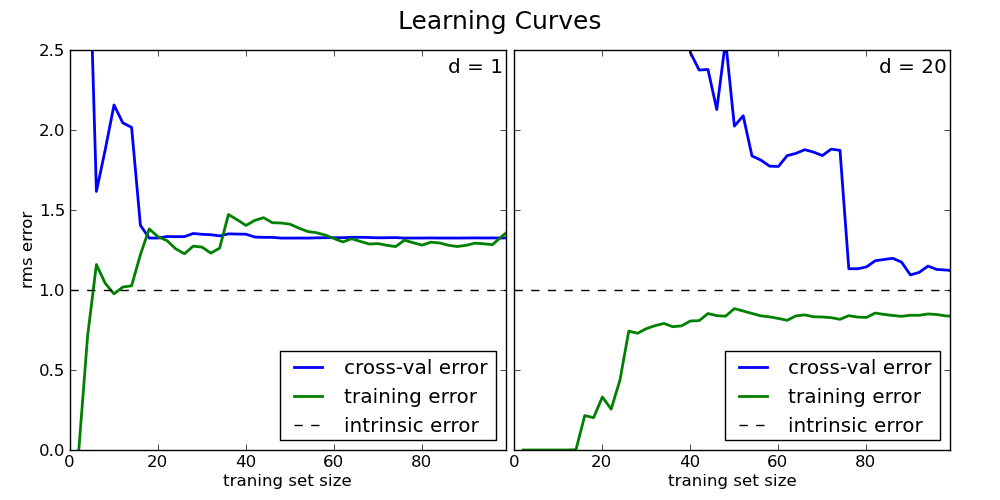
Learning Curves for a case of high bias (left, d = 2) and high variance (right, d = 20)
-
Sur la gauche, le polynôme de degré 1 est un estimateur hautement biaisé qui sous-apprend les données. C’est indiqué par le fait qu’à la fois les erreurs d’entrainement et les erreurs de cross-validation sont élevées.
-
Sur la droite, le polynôme est de degré 20. L’erreur d’entrainement est beaucoup plus faible que l’erreur de cross-validation. Plus on ajoute de données dans le training set et plus l’erreur d’entrainement augmente alors que l’erreur de cross-validation diminue.
Conclusion
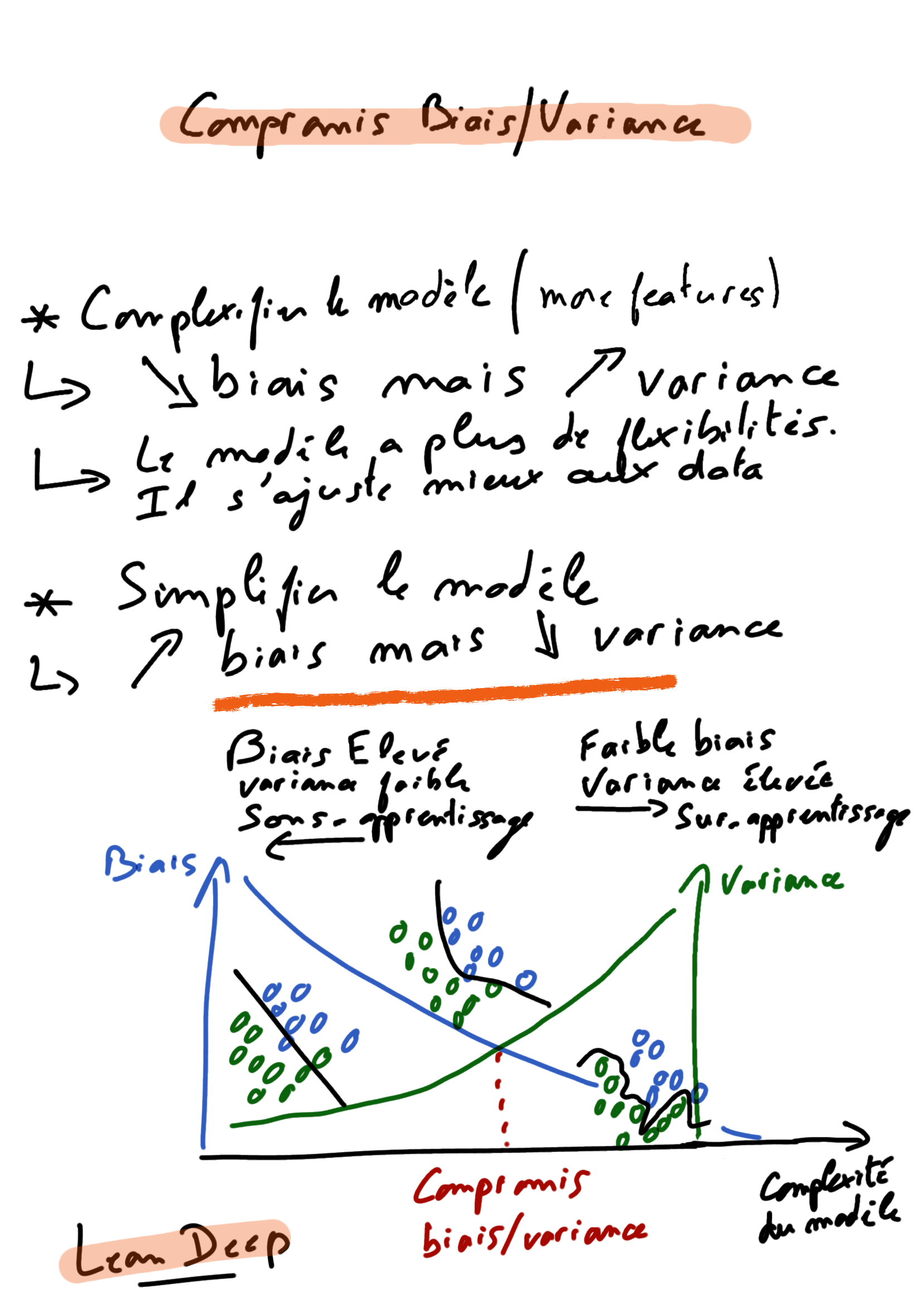
Fort biais
Si notre algorithme montre un fort biais, il faut:
- Ajouter plus de features
- Utiliser un modèle plus sophistiqué
- Diminuer le training set pour booster la durée d’entrainement. On arrivera à la même erreur plus rapidement; avec moins de données d’entrainement. Par contre, cela ne va pas améliorer la classification.
- Diminuer la régularisation: la régularisation est une technique utilisée pour simplifier certains modèles de Machine Learning en ajoutant des termes de pénalité qui dépendent des caractéristiques des paramètres.
Forte variance
- Utiliser moins de features
- Augmenter le training set. Ajouter des données dans le training set peut réduire l’effet d’over-fitting et conduire à diminuer la variance de l’estimateur.
- Augmenter la régularisation qui est faite justement pour éviter l’over-fitting.
Code des graphs
import pylab as pl
from matplotlib import ticker
from matplotlib.patches import FancyArrow
np.random.seed(42)
def test_func(x, err=0.5):
return np.random.normal(10 - 1. / (x + 0.1), err)
def compute_error(x, y, p):
yfit = np.polyval(p, x)
return np.sqrt(np.mean((y - yfit) ** 2))
#------------------------------------------------------------
# Plot linear regression example
np.random.seed(42)
x = np.random.random(20)
y = np.sin(2 * x)
p = np.polyfit(x, y, 1) # fit a 1st-degree polynomial to the data
xfit = np.linspace(-0.2, 1.2, 10)
yfit = np.polyval(p, xfit)
pl.scatter(x, y, c='k')
pl.plot(xfit, yfit)
pl.xlabel('x')
pl.ylabel('y')
pl.title('Linear Regression Example')
#------------------------------------------------------------
# Plot example of over-fitting and under-fitting
N = 8
np.random.seed(42)
x = 10 ** np.linspace(-2, 0, N)
y = test_func(x)
xfit = np.linspace(-0.2, 1.2, 1000)
titles = ['d = 1 (under-fit)', 'd = 2', 'd = 6 (over-fit)']
degrees = [1, 2, 6]
pl.figure(figsize = (9, 3.5))
for i, d in enumerate(degrees):
pl.subplot(131 + i, xticks=[], yticks=[])
pl.scatter(x, y, marker='x', c='k', s=50)
p = np.polyfit(x, y, d)
yfit = np.polyval(p, xfit)
pl.plot(xfit, yfit, '-b')
pl.xlim(-0.2, 1.2)
pl.ylim(0, 12)
pl.xlabel('house size')
if i == 0:
pl.ylabel('price')
pl.title(titles[i])
pl.subplots_adjust(left = 0.06, right=0.98,
bottom=0.15, top=0.85,
wspace=0.05)
#------------------------------------------------------------
# Plot training error and cross-val error
# as a function of polynomial degree
Ntrain = 100
Ncrossval = 100
error = 1.0
np.random.seed(0)
x = np.random.random(Ntrain + Ncrossval)
y = test_func(x, error)
xtrain = x[:Ntrain]
ytrain = y[:Ntrain]
xcrossval = x[Ntrain:]
ycrossval = y[Ntrain:]
degrees = np.arange(1, 21)
train_err = np.zeros(len(degrees))
crossval_err = np.zeros(len(degrees))
for i, d in enumerate(degrees):
p = np.polyfit(xtrain, ytrain, d)
train_err[i] = compute_error(xtrain, ytrain, p)
crossval_err[i] = compute_error(xcrossval, ycrossval, p)
pl.figure()
pl.title('Error for 100 Training Points')
pl.plot(degrees, crossval_err, lw=2, label = 'cross-validation error')
pl.plot(degrees, train_err, lw=2, label = 'training error')
pl.plot([0, 20], [error, error], '--k', label='intrinsic error')
pl.legend()
pl.xlabel('degree of fit')
pl.ylabel('rms error')
pl.gca().add_patch(FancyArrow(5, 1.35, -3, 0, width = 0.01,
head_width=0.04, head_length=1.0,
length_includes_head=True))
pl.text(5.3, 1.35, "High Bias", fontsize=18, va='center')
pl.gca().add_patch(FancyArrow(19, 1.22, 0, -0.1, width = 0.25,
head_width=1.0, head_length=0.05,
length_includes_head=True))
pl.text(19.8, 1.23, "High Variance", ha='right', fontsize=18)
#------------------------------------------------------------
# Plot training error and cross-val error
# as a function of training set size
Ntrain = 100
Ncrossval = 100
error = 1.0
np.random.seed(0)
x = np.random.random(Ntrain + Ncrossval)
y = test_func(x, error)
xtrain = x[:Ntrain]
ytrain = y[:Ntrain]
xcrossval = x[Ntrain:]
ycrossval = y[Ntrain:]
sizes = np.linspace(2, Ntrain, 50).astype(int)
train_err = np.zeros(sizes.shape)
crossval_err = np.zeros(sizes.shape)
pl.figure(figsize=(10, 5))
for j,d in enumerate((1, 20)):
for i, size in enumerate(sizes):
p = np.polyfit(xtrain[:size], ytrain[:size], d)
crossval_err[i] = compute_error(xcrossval, ycrossval, p)
train_err[i] = compute_error(xtrain[:size], ytrain[:size], p)
ax = pl.subplot(121 + j)
pl.plot(sizes, crossval_err, lw=2, label='cross-val error')
pl.plot(sizes, train_err, lw=2, label='training error')
pl.plot([0, Ntrain], [error, error], '--k', label='intrinsic error')
pl.xlabel('traning set size')
if j == 0:
pl.ylabel('rms error')
else:
ax.yaxis.set_major_formatter(ticker.NullFormatter())
pl.legend(loc = 4)
pl.ylim(0.0, 2.5)
pl.xlim(0, 99)
pl.text(98, 2.45, 'd = %i' % d, ha='right', va='top', fontsize='large')
pl.subplots_adjust(wspace = 0.02, left=0.07, right=0.95)
pl.suptitle('Learning Curves', fontsize=18)
pl.show()