Dans cet article nous allons voir comment classifier des chiffres écrits à la main. Le dataset que nous allons utiliser est publique, bien connu et accessible depuis scikit. Nous allons voir le processus pour classifier ces chiffres et voir comment évaluer la performance de notre modèle.

from sklearn.datasets import load_digits
digits = load_digits()
print(digits.data.shape)
(1797, 64)

Notre dataset contient 1797 échantillons.

On affiche les 128 premiers échantillons sur un graphique de 9x9 pouces.

fig = plt.figure(figsize=(9, 9))  # figure size in inches
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)

# plot the digits: each image is 8x8 pixels
for i in range(128):
    ax = fig.add_subplot(16, 8, i + 1, xticks=[], yticks=[])
    ax.imshow(digits.images[i], cmap=plt.cm.binary, interpolation='nearest')
    
    # label the image with the target value
    ax.text(0, 7, str(digits.target[i]))

Résultat:

Visualisation des données

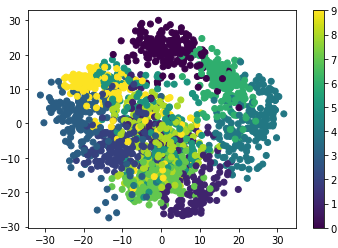
Pour beaucoup de problème, la première étape est de visualiser les données en utilisant une technique de réduction de dimensions. Pour ce faire, l’algorithme le plus simple est PCA (Principal Component Analysis)

Cet algorithme cherche à trouver les combinaisons linéaires orthogonales qui ont la plus grande variance entre les features du dataset. Cela permet d’avoir une bonne idée de la structure du dataset.

from sklearn.decomposition import RandomizedPCA
pca = RandomizedPCA(n_components=2)
proj = pca.fit_transform(digits.data)

plt.scatter(proj[:, 0], proj[:, 1], c=digits.target)
plt.colorbar()

Résultat:

Classifieur naïf bayésien

A la base de la classification naïve bayésienne se trouve le théorème de Bayes avec l’hypothèse simplificatrice, dite naïve, d’indépendance entre toutes les paires de variables. Le rôle de ce classifieur est de classer dans des groupes (des classes) les échantillons qui ont des propriétés similaires, mesurées sur les observations.

Ce classifieur simple permet d’avoir rapidement une idée de nos données. Dans notre cas, il se prête au sujet mais avec des données plus complexe, il faut passer à un classifieur plus sophistiqué.

from sklearn.naive_bayes import GaussianNB
from sklearn.cross_validation import train_test_split

# split des données en 2 parties: apprentissage et test
X_train, X_test, y_train, y_test = train_test_split(digits.data, digits.target)

# Entrainement du modèle
clf = GaussianNB()
clf.fit(X_train, y_train)

# On utilise le modèle pour prédire les labels des données de test
predicted = clf.predict(X_test)
expected = y_test

On réaffiche les chiffres avec la prédiction de notre classifieur. Si le chiffre est en vert, cela signifie que notre classifieur a bien trouvé le bon chiffre. En rouge, il s’est trompé.

fig = plt.figure(figsize=(9, 9))  # Taille du graphique en pouces
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)

# On affiche les chiffres: chaque image fait 16x16 pixels
for i in range(128):
    ax = fig.add_subplot(16, 16, i + 1, xticks=[], yticks=[])
    ax.imshow(X_test.reshape(-1, 8, 8)[i], cmap=plt.cm.binary,
              interpolation='nearest')
    
    # On labelise l'image avec la valeur prédite
    if predicted[i] == expected[i]:
        ax.text(0, 7, str(predicted[i]), color='green')
    else:
        ax.text(0, 7, str(predicted[i]), color='red')

Résultat:

Mesure quantitative de la performance du classifieur

Une première approche simple consisterait à calculer le pourcentage de bonnes prédictions du classifieur.

matches = (predicted == expected)
print(matches.sum())
print(len(matches))

matches.sum() / float(len(matches))

Résultat:

372
450

0.88222222222222224

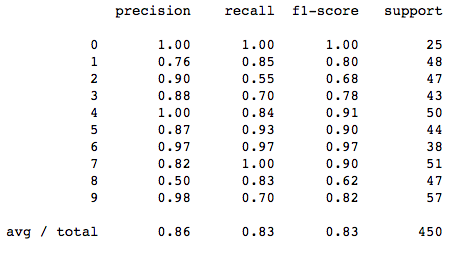
Ce résultat est pas trop mal mais d’autres métriques plus sophistiquées peuvent être utilisées pour juger de la performance du classifieur. Les métriques données par ==classification_report== peuvent être utilisées. Cet outil est disponible dans le package ==sklearn.metrics==.

from sklearn import metrics
print(metrics.classification_report(expected, predicted))

Résultat:

La matrice de confusion (ou tableau de contingence) peut également nous donner des précisions sur la performance de notre classifieur. Elle est obtenue en comparant les données classées avec des données de référence qui doivent être différentes de celles ayant servi à réaliser la classification.

print(metrics.confusion_matrix(expected, predicted))

Résultat:

[[25  0  0  0  0  0  0  0  0  0]
 [ 0 41  1  0  0  0  0  0  5  1]
 [ 0  3 26  1  0  0  0  0 17  0]
 [ 0  0  2 30  0  2  0  1  8  0]
 [ 0  3  0  0 42  1  1  2  1  0]
 [ 0  0  0  1  0 41  0  1  1  0]
 [ 0  1  0  0  0  0 37  0  0  0]
 [ 0  0  0  0  0  0  0 51  0  0]
 [ 0  5  0  2  0  1  0  0 39  0]
 [ 0  1  0  0  0  2  0  7  7 40]]

Explications sur la lecture de cette Matrice:

     0  1  2  3  4  5  6  7  8  9 (classe estimée)
0 [[25  0  0  0  0  0  0  0  0  0]
1  [ 0 41  1  0  0  0  0  0  5  1]
2  [ 0  3 26  1  0  0  0  0 17  0]
3  [ 0  0  2 30  0  2  0  1  8  0]
4  [ 0  3  0  0 42  1  1  2  1  0]
5  [ 0  0  0  1  0 41  0  1  1  0]
6  [ 0  1  0  0  0  0 37  0  0  0]
7  [ 0  0  0  0  0  0  0 51  0  0]
8  [ 0  5  0  2  0  1  0  0 39  0]
9  [ 0  1  0  0  0  2  0  7  7 40]]

• Sur 25 chiffres prédits à 0, il n’y a pas eu d’erreur

• Verticalement, sur 53 chiffres prédits à 1, (additionner verticalement: 41+3+3+1+5 = 53)

  • 3 étaient en fait des 2,
  • 3 étaient des 4
  • 1 chiffre prédit à 1 était en fait un 6
  • 5 étaient des 8
  • Soit un total de 12 erreurs

• Verticalement, sur 71 chiffres prédits à 8, seulement 39 sont bons

  • 17 étaient en fait des 2
  • 8 étaient des 3
  • 39 erreurs de prédictions quand le classifieur a estimé des chiffres à 8

• Horizontalement, sur 47 chiffres qui étaient à 2, 26 sont biens estimés

• Horizontalement, sur 43 chiffres qui étaient des 3, 30 sont biens estimés

Ce qu’on voit surtout en conclusion, c’est les chiffres 1, 2, 3, et 9 sont souvent labelisé comme des 8.