Introduction, la révélation

Nous sommes avril 2015, je reviens de mes vacances à Rome. (Franchement je recommande cette ville mais parler de Rome n’est pas le sujet de cet article). Pendant mes vacances, j’ai eu le temps de réfléchir sur ce que je voulais faire et j’ai eu une révélation. Je veux faire du Machine Learning !

C’est une discipline que je ne connais pas du tout et qui a l’air vraiment cool. Le sujet a l’air extrèmement vague et je ne sais pas vraiment par où commencer.

J’ai commencé par revoir quelques bases en statistique; même si je ne suis pas certain que cette discipline soit le même. J’ai vu qu’il y avait un cours sur Coursera pour sur le sujet. C’est un cours de 9 semaines. Je pense que je vais le suivre.

Peut-être que vous aussi vous avez bouffé mangé des maths pendant vos études mais que vous n’avez pas pratiqué depuis longtemps et donc que des rappels ne feront pas de mal.

Rappels de stats

Espérance

Lorsqu’on a des données statistiques, l’espérance correspond à la moyenne de ces données.

Caractéristiques de dispersion

La variance et l’écart type permettent de mesurer la « dispersion » des valeurs de la série autour de l’espérance (ou de la moyenne). Si les valeurs de la série possèdent une unité, l’écart type s’exprime dans la même unité.

Variance

Pour quantifier la dispersion d’une série par rapport à sa moyenne, il semble naturel de calculer la moyenne des différences (ou des écarts) entre les valeurs observées et la moyenne, mais avec le risque d’obtenir des nombres négatifs qui, ajoutés à des nombres positifs, s’annulent. C’est pourquoi on a choisi de calculer la « moyenne des carrés des écarts à la moyenne ». Telle est la définition de la variance V d’une série statistique.

Calcul de la variance (2 options):

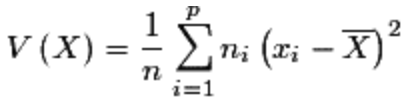
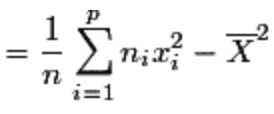
Écart-type

L’écart-type est un indicateur de dispersion. Il nous informe sur la manière dont les individus se répartissent autour de la moyenne. Sont-ils tous à peu près identiques, concentrés autour de la moyenne ? Au contraire, sont-ils dispersés entre des valeurs très basses et des valeurs très hautes ?

L’écart-type est l’écart moyen à la moyenne pour tous les individus. Si celui-ci est faible, les individus formulent des réponses similaires, si celui-ci est fort les variations sont fortes dans la population étudiée. Le niveau qui permet de repérer un fort écart-type est 1/2 moyenne. Si l’écart-type est supérieur à 0,5 moyenne, on peut donc considérer que les variations sont fortes.

Pour illustrer nos propos, prenons un exemple simple. 21 étudiants reçoivent une note sur 20 en statistique, les voici :

1 - 3 - 3 - 4 - 4 - 6 - 7 - 8 - 9 - 9 - 9 - 9 - 9 - 10 - 10 - 15 - 17 - 18 - 19 - 20 - 20

Moyenne = 10 (210/21) Ecart-type = 5,93.

Dans ce cas, la dispersion est forte puisque l’écart-type est supérieur à 5 (1/2 moyenne).

Formule de calcul:

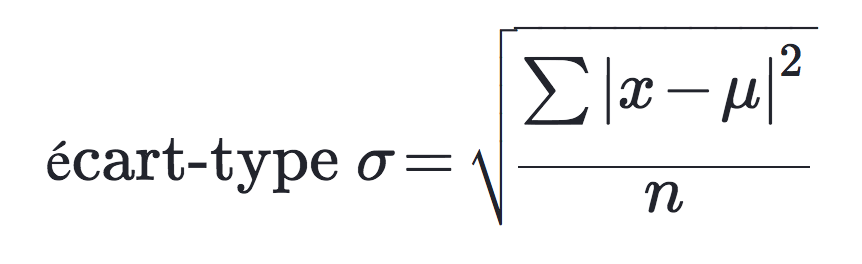
• avec μ est la moyenne arithmétique de la série
• n est l’effectif total de la série

Autre formule de calcul:

C’est un paramètre particulièrement utilisé dans le cas de données dites gaussiennes.

Données Gaussiennes

Les données gaussiennes se caractérisent par une répartition en forme de cloche. Elles ont l’allure suivante:

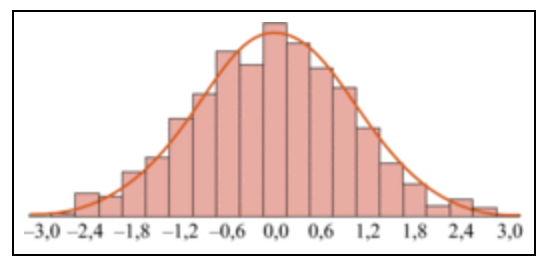
Dans le cas de données gaussiennes, la médiane et la moyenne sont confondues. La médiane est, de plus, le milieu de l’intervalle interquartile ; ainsi, le corps du diagramme qui représente les données est symétrique par rapport à la médiane.

Médiane

Définition: L’idée générale est que la médiane est une valeur du caractère qui partage la population en deux parties de même effectif. De façon plus précise, on appelle médiane d’une série statistique discrète toute valeur M du caractère telle qu’au moins 50% des individus aient une valeur du caractère inférieure ou égale à M et au moins 50% des individus aient une valeur du caractère supérieure ou égale à M

Recherche pratique de la médiane: On range les valeurs du caractère une par une dans l’ordre croissant (chaque valeur du caractère doit apparaître un nombre de fois égal à l’effectif correspondant). Si l’effectif total est impair, la médiane M est la valeur du caractère située au milieu. Si l’effectif total est pair, la médiane M est la demi-somme des 2 valeurs situées au milieu.

Example 1: Liste des valeurs du caractère :

7 ; 7 ; 8 ; 9; 10 ; 11 ; 11 ; 14 ; 16 ; 16

L’effectif total est pair : la médiane M est la demi-somme des 2 valeurs situées au milieu. D’où, M = (10 + 11) / 2 = 10,5

Example 2:

6 ; 6 ; 6 ; 8; 9 ; 9 ; 12 ; 13 ; 13 ; 13 ; 17 ; 17; 17

L’effectif total est impair : la médiane M est la valeur située au milieu. D’où, M = 12.

Paramètres de dispersion

Définition: Ces paramètres permettent de mesurer la façon dont les valeurs du caractère sont réparties autour de la moyenne et de la médiane.

Paramètre de dispersion associé à la médiane: L’idée générale est de partager la population en quatre parties de même effectif.

Etant donné une série statistique de médiane M dont la liste des valeurs est rangée dans l’ordre croissant En coupant la liste en deux sous-séries de même effectif (Attention : quand l’effectif total est impair, la médiane ne doit pas être incluse dans les sous-séries) :

• On appelle premier quartile le réel noté Q1 égal à la médiane de la sous-série inférieure.
• On appelle troisième quartile le réel noté Q3 égal à la médiane de la sous-série supérieure.
• L’écart interquartile est égal à Q3 - Q1.
• ] Q1 ; Q3 [ est appelé intervalle interquartile.

Diagramme en boîtes: Le diagramme en boîtes d’une série statistique se construit alors de la façon suivante : (les valeurs du caractère sont en abscisse - min et max représentent les valeurs minimales et maximales du caractère)

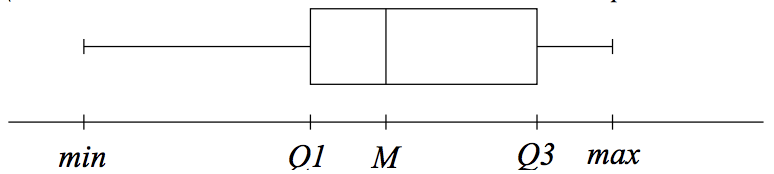
Interprétation:

• 25% de la population admet une valeur du caractère entre min et Q1
• 25% de la population admet une valeur du caractère entre Q1 et M
• 25% de la population admet une valeur du caractère entre M et Q3
• 25% de la population admet une valeur du caractère entre Q3 et max

Test du χ²

Le test de Chi-deux est utilisé pour tester l’hypothèse nulle d’absence de relation entre deux variables catégorielles. On peut également dire que ce test vérifie l’hypothèse d’indépendance de ces variables.

En statistique, le test du χ² de Pearson ou test du χ² d’indépendance est un test statistique qui s’applique sur des ensembles de données catégorielles pour évaluer la probabilité qu’une différence observée entre les ensembles soit due au hasard. Il convient aux données non-appariées prises sur de grands échantillons (n>30). Il est le test du χ² le plus communément utilisé.

Population et individus

La population est l’ensemble des individus (ou unités statistiques) auxquels on décide de sintériser. Sa taille, habituellement désignée par N, est grande, ou même infinie. Le choix de la population étudiée dépend du problème qui est à l’origine de la démarche statistique, et de la façon dont on décide de le traiter.

Effectif

Nombre d’individus, d’une population ou d’une partie quelconque de cette population.

Représentations géométriques des distributions

• Pour une variable qualitative : diagramme circulaire (“camembert”).
• Pour une variable ordinale ou quantitative discrète : diagramme ou graphique en bâtons.
• Pour une variable ordinale ou quantitative continue : histogramme et courbe des fréquences cumulées.
• Pour deux variables quantitatives ou ordinales : nuage de points.

Distribution Multimodale

Il s’agit d’une distribution qui possède plusieurs modes (donc au moins deux “pics”).

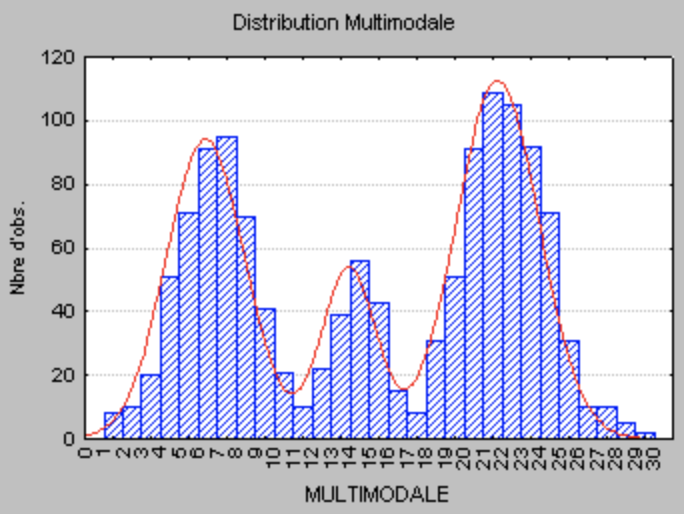
La multimodalité d’une distribution dans un échantillon indique généralement que la distribution de la variable dans la population n’est pas normale. La multimodalité d’une distribution peut fournir une information importante quant à la nature de la variable étudiée (c’est-à-dire la qualité mesurée). Par exemple, si la variable en question représente une préférence ou une attitude déclarée, la multimodalité peut indiquer qu’il existe plusieurs points de vue ou structures de réponse dans le questionnaire. Toutefois, dans la plupart des cas, la multimodalité indique que l’échantillon n’est pas homogène et que les observations proviennent de deux distributions (ou davantage) qui se “chevauchent”. Parfois, la multimodalité d’une distribution peut révéler des problèmes au niveau de l’instrument de mesure (par exemple, des “problèmes de calibration de l’appareil” en sciences naturelles ou un “biais dans les réponses” en sciences sociales).